The Gavrog Project

Gavrog stands for Generation, Analysis and Visualization of Reticular Ornaments using Gavrog. It is about pretty pictures, solid state chemistry and rather involved mathematics. Think Escher, crystals, Alhambra, soap bubbles. If you find the pictures on this page interesting, or appealing, you might like to check it out.

Software

The purpose of Gavrog is to develop an integrated Java library for nets (a.k.a. graphs) and other structures that can be described in terms of nets - the reticular aspect - which are situated (mostly) in ordinary space and show a high geometric symmetry - the ornament aspect. Examples of these are crystal nets, periodic ornaments and both 2- and 3-dimensional tilings, as shown below and to the left.

Currently, while some components of Gavrog can be considered fairly mature, others are in varying stages of development. There is a pretty comprehensive, usable and well-tested library for topological analysis and structure generation. The program Systre has consistently been reported as very stable and reliable. Its cousin 3dt on the other hand, while useful and fun to play with, may still be considered somewhat "rough around the edges".

Gavrog is written in Java and thus needs a Java runtime environment (JRE) of version 1.5.0 or later to work. Java is included in the latest version of Mac OS X and, for other operating systems, may have been installed previously as a prerequisite for another program. If this is not the case, you can download a JRE from http://java.com.

If you are interested in the current source code, please visit our GitHub repository.

Systre

The program Systre is designed to analyze periodic nets as they arise in the study of (extended or non-molecular) crystal structures. The acronym stands for Symmetry, Structure (Recognition) and Refinement. The Gavrog version of Systre is closely modeled after an earlier experimental version of the program written in Python.

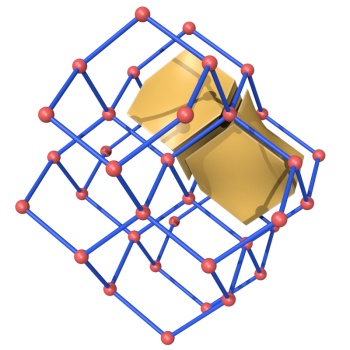
Systre uses a method called barycentric placement to determine the ideal (i.e., maximal embeddable) symmetry of a crystal net and to analyze its topological structure. It then generates a unique key for the topological type of the given net and uses this key to look up the structure in its built-in database. Systre also computes a new embedding of the net which exhibits the ideal symmetry.

Systre's built-in database contains 176 recognized zeolite framework types and most of the more than thousand nets contained in the Reticular Chemistry Structure Resource (RCSR). Zeolite frameworks are identified by a three-letter code in capital letters, while RCSR nets are identified by a three-letter code in lower letters. Users can also create their own databases and will in a future version be able use the Systre key to look up structures in several online databases.

Examples of projects that already use Systre are the EPINET project at the Australian National University and the Reticular Chemistry Structure Resource (RCSR) hosted at the Australian National University in collaboration with Arizona State University and the University of California at Los Angeles.

Systre Systre 1.1.5 is the latest release. This version is, unfortunately, text-only, but code for interactively displaying nets is under development.

• View instructions on installing and using Systre

The graphical user interface for Systre is based on the Bouy library, which is available at buoy.sourceforge.net. Bouy is now included in the Gavrog source code and need no longer be installed separately.

3dt

3dt is the latest in a long line of tiling visualization programs based on combinatorial tiling theory and utilizing so-called Delaney-Dress symbols (see references below).

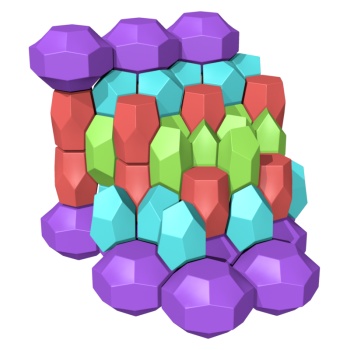
A tiling is a partition of space into tiles that are topological cells — bounded bodies without holes. We are mostly interested in tilings that are periodic, i.e., based on a repetitive pattern. Two-dimensional examples are easily found in daily life, such as the surfaces of brick walls and pavings. In three dimensions, (dry) foams make nice examples of — typically non-periodic — tilings.

The original 3dt, written in Python, started out around 1996 as a partial three-dimensional counterpart to Daniel Huson's program 2dTiler. It had a GUI written in Tkinter and used Geomview as its render engine. Although a handful of people have been using that version successfully in their daily work, I never considered the code base mature enough for a public release.

Gavrog 3dt is written entirely in Java and relies only on Java software, which makes it very portable. Its graphics engine is based on the open-source visualization library jReality which is being developed at the Technische Universität Berlin. The multitude of backends provided by jReality make it easy to produce a variety of output styles such as stereographic image-pairs or photorealistic raytrace renders. In fact, all the images on this page were rendered with Sunflow, an open source raytracer that comes integrated with 3dt.

• View instructions on using 3dt

Some Background

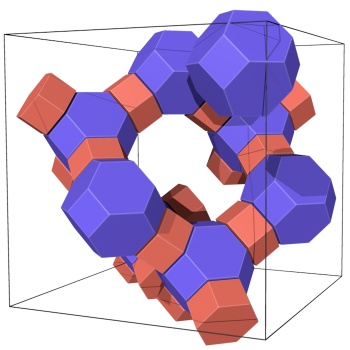
The Gavrog project is concerned with geometric objects such as point clouds, periodic nets, tilings and polyhedra. The following links (more to come) provide some background on what these are and how the Gavrog software represents and manipulates them. Please be aware that large parts of these texts were written for specialists.

• When is a Crystal Graph not Crystallographic? - Talk from December 2019 about periodic graphs and their combinatorial symmetry groups. (PDF 4.1MB)
• Analyzing Periodic Nets via the Barycentre Construction - Lecture on the inner workings of Systre held in Santa Barbara in August 2008 (PDF 1.4MB)
• Some Elementary Tiling Theory - Lecture held in Santa Barbara in August 2008 (PDF 1.2MB)
• Data Structures and Algorithms for Tilings - Covers some computational aspects of tiling theory. (PDF 170KB)
• Crystal Topologies and Discrete Mathematics - Slides for a talk held in Leipzig in October 2004. (PDF 2.9MB)
• Periodic Graphs and a Result by Tutte - Slides for a talk held in Heidelberg in September 2004 (english text, only the title page is in German). (PDF 1.7MB)